TUM Science Hackathon

Astrid Eckert/ TUM

We will offer a challenge touching advanced cybersecurity technologies at the TUM Science Hackathon organized by TUM: Junge Akademie.

Registration

To register for the hackathon with the intent to work on the challenge offered by us, two separate registrations are required:

• Register for the hackathon at the official TUM Science Hackathon website. You need to register officially for the hackathon to participate and get updates from the organizers. This step is mandatory.

• To get informed about the hackathon challenge from the Cybersecurity Polygon Program team and to become eligible for the option to obtain a program certificate, please also register by following the instructions on the registration page.

Advanced Security-enhancing Technologies: Trust in Action

“Advanced Security-enhancing Technologies: Trust in Action” challenges you to explore the next generation of advanced secure systems by combining cutting-edge technologies that protect data confidentiality and integrity. By prototyping solutions that combine Trusted Execution Environments (TEEs), Secure Multiparty Computation (SMC), and Zero-Knowledge Proofs (ZKP), you are challenged to address real-world problems—from safeguarding AI algorithms and sensitive financial data to enabling secure, privacy-preserving collaborations. Those primitives have been focus topics within recent security and cryptography research and are now ready to be used in practice. Especially in a world where AI is becoming increasingly integrated into our daily lives, those primitives could be applied to a wide range of issues such as privacy and data protection, data provenance to prevent the spread of misinformation, ensuring the integrity of data streams, and many more.

Building Blocks: A Brief Introduction

We intend to provide you with materials and resources to get you started with the basics of TEEs, SMC, and ZKP, including hardware access and references to libraries and tutorials. We will also be present at the hackathon in person to help you out. If you are unfamiliar with those topics, here is a brief introduction.

Trusted Execution Environments (TEEs)

Trusted Execution Environments (TEEs) are secure, isolated areas within a processor that protect sensitive data and code during execution. They create a hardware-enforced “safe zone” that even a compromised operating system cannot access. TEEs ensure both the confidentiality and integrity of the data processed inside them by using hardware-backed encryption keys and secure boot mechanisms. One key feature of TEEs is remote attestation, which allows a remote party to verify that the TEE is running the expected, untampered code on trusted hardware.

TEEs have various applications—from protecting sensitive computations in cloud environments to securing mobile devices. Popular implementations include Intel SGX, Intel TDX, ARM TrustZone and AMD SEV. Those platforms offer different trade-offs between security, usability, and performance. By running critical code inside a TEE, risks associated with malware or unauthorized system modifications by an attacker can be mitigated.

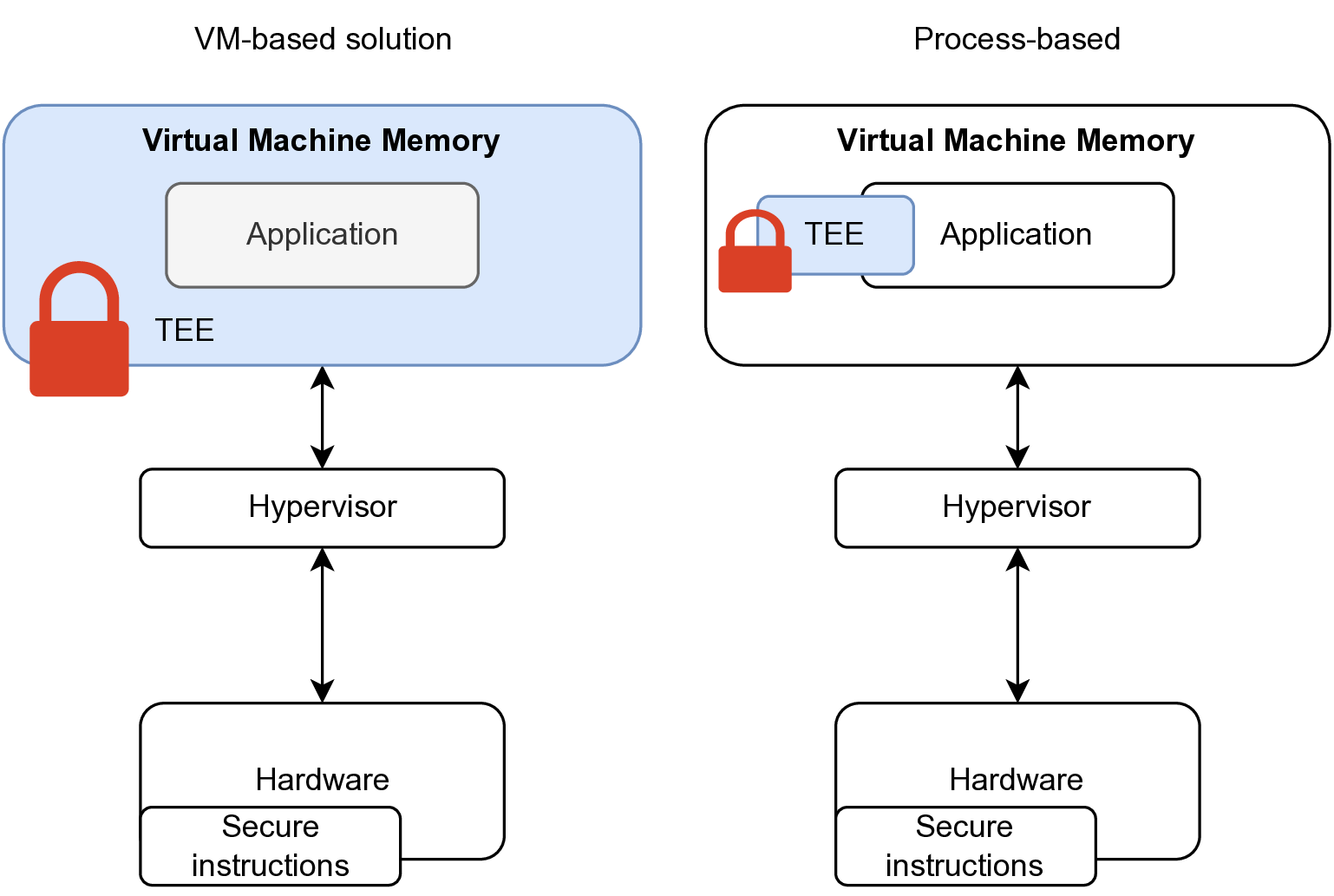
TEE architectures can be categorized into process-based TEEs (Intel SGX, ARM TrustZone), which secure individual application processes, and VM-based TEEs (Intel TDX, AMD SEV), which isolate entire virtualized environments—each approach offering unique benefits and trade-offs. The following figure illustrates the differences between the two architectural approaches.

Secure Multiparty Computation (SMC)

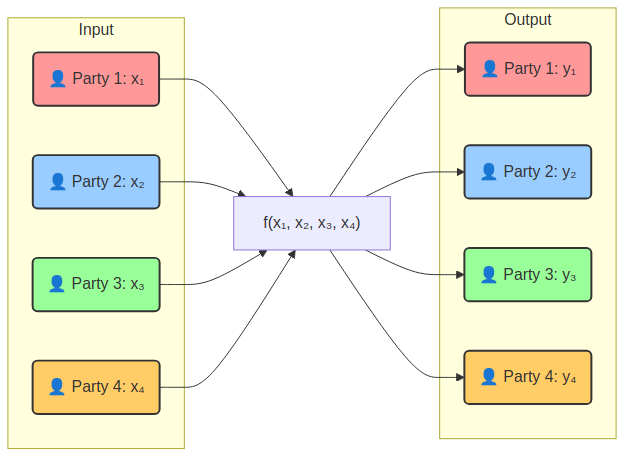
Secure Multiparty Computation (SMC) is a cryptographic technique that enables multiple parties to jointly compute a function over their private inputs without revealing those inputs to one another. In essence, SMC allows participants—each holding confidential data—to collaborate on a computation, with the only shared outcome being the final result.

The key idea is that the parties exchange “shares” of their data or perform computations on encrypted values, ensuring that no single party ever sees the full input of other parties. Protocols like Yao’s garbled circuits (for two-party computations) and secret sharing-based methods (such as those using Shamir’s secret sharing for multiparty setups) form the basis of SMC implementations. This technology is a very useful tool when privacy is paramount to an application, such as collaborative data analytics, secure voting systems, or joint financial computations, where each party’s input must remain confidential.

Zero-Knowledge Proofs (ZKP)

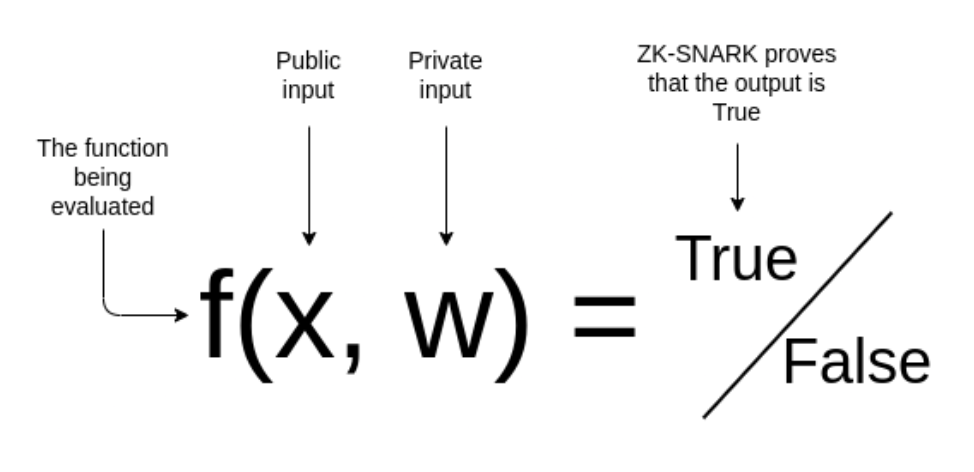
Zero-knowledge proofs (ZKPs) are cryptographic protocols that enable one party, the prover, to convince another party, the verifier, that a statement is true without revealing any additional information about the prover’s input. This capability is especially valuable in contexts where confidentiality is a strong requirement. An example scenario could be a user wanting to prove their solvency without revealing their full financial data.

A widely adopted variant of ZKPs are (zk)SNARKs—Succinct Non-interactive Arguments of Knowledge. SNARKs produce very short proofs (between ~200B and a few KB, depending on the algorithm) that are efficient to verify, making them ideal for applications that require scalability and fast validation. SNARKs enable another interesting use case, which is the ability to prove the correctness of a computation without the verifier having to do the full computation by himself. Example use cases include outsourcing computation to a semi-trusted third party or scaling up blockchains.

Building on SNARKs, which are notoriously difficult to understand, general-purpose zero-knowledge virtual machines (zkVMs) make the power of ZKPs available to non-cryptographers. General-purpose zkVMs allow developers to write and execute programs in high-level languages (e.g., Rust) while automatically generating a proof of correct execution. This proof verifies that the prover performed the computation accurately without exposing any sensitive data involved in the process. While SNARKS can theoretically prove any computation, e.g., the inference step of a neural network on encrypted data, such use cases are often not yet practical regarding prover overhead.

Vitalik Buterin